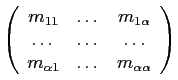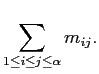Now adding an edge we should distinguish between the loops and the
edges connecting different vertices. Adding a loop to the vertex ![]() we have to
replace
we have to
replace ![]() by
by ![]() . Adding an edge that connects
. Adding an edge that connects ![]() with
with
![]() , where
, where ![]() , we have to replace both
, we have to replace both ![]() and
and ![]() by
by ![]() and
and ![]() , correspondingly. Note that by induction it follows that
, correspondingly. Note that by induction it follows that
![]() for all
for all ![]() .
.