1.2.1 Connectedness

There is an easy way to tell by an incidence matrix whether a graph is connected.

Example 1.2.3   Numerate the vertices of the graph

\begin{picture} % latex2html id marker 220 (100.00,50.00) \put(-5,20){\circle*{2... ...,-1){30}} \put(-15,20){\circle{20}} \qbezier(85,40)(110,30)(105,0) \end{picture}
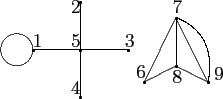
in such a way that the vertices of one component have numbers from 1 to 5, and the vertices of the other - from 6 to 9:

\begin{picture} % latex2html id marker 242 (100.00,50.00) \put(-5,20){\circle*{2... ...,-1){30}} \put(-15,20){\circle{20}} \qbezier(85,40)(110,30)(105,0) \end{picture}
Then the incidence matrix is

% latex2html id marker 4863 $\displaystyle \left(\begin{array}{ccccccccc} 1 & 0... ... & 0 & 1 & 1 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 2 & 1 & 0 \end{array}\right) $

The following lemma is well-known and can be easily established:

Lemma 1.2.4   The graph is disconnected if and only if its vertices can be numerated in such a way that its incidence matrix is of the block form.

Exercise 1.2.5   Draw a disconnected graph consisting of two connected ones, each having two vertices. Numerate the four vertices in such a way that its incidence matrix is not of the block form. Then renumber them in all the possible ways and write down all the incidence matrices. How much of them will be of the block form?